Zinseszins und die 72er-Regel
Du hast bestimmt schonmal vom Zinseszins gehört. Ich habe ihn in diesem Beitrag kurz erwähnt.
Manche Menschen finden Zinseszins unmoralisch. Das sehe ich nicht so. Wucher, also extrem hohe Zinsen (oder Preise), finde ich unmoralisch. Normale Zinsen sind einfach die Leihgebühr, die ich für geliehenes Geld zahle.
Lass es mich an einem Beispiel deutlich machen:
Angenommen, Julia* hat eine grandiose Idee für eine Unternehmensgründung. Um diese Idee umzusetzen, braucht sie 1.000€ Startkapital. Leider hat sie keine Rücklagen und kann das Projekt alleine nicht starten.
Anna* hat ein diszipliniertes Budget und genug Rücklagen. Sie leiht Julia gerne 1.000€.
Die beiden verabreden, dass Anna Julia die 1.000€ für ein Jahr leiht. Als Dank zahlt Julia ihr am Ende des Jahres das Geld zurück, plus 10% Zinsen. 10% von 1.000€ sind 100€; das ist die Leihgebühr, die Julia für Annas Geld zahlt.
Nach einem Jahr hat Julia mit ihrem Unternehmen Gewinn gemacht. Sie zahlt Anna wie verabredet die 1.000€ plus 100€ (10%) Zinsen, also insgesamt 1.100€, zurück.
Nach diesem ersten Jahr hat Julia weitere Ideen, wie sie ihr Unternehmen weiterentwickeln kann. Hierfür muss sie neue Technik kaufen (z.B. eine Videokamera, um gute Videos für ihren Online-Kurs aufnehmen zu können). Anna bietet ihr an, ihr wieder Geld zu leihen.
Da Anna jetzt 1.100€ übrig hat (das Geld, das sie von Julia zurückbekommen hat), gibt sie ihr gerne das ganze Geld. Sie verabreden wieder 10% Leihgebühr, also Zinsen. Nach einem Jahr zahlt Julia Anna die geliehenen 1.100€ zurück, plus 10% Zinsen. 10% von 1.100€ sind 110€. Julia zahlt nach dem zweiten Jahr also 1.100€ + 110€ = 1.210€ an Anna.
Im ersten Jahr hat Anna 100€ Leihgebühr bekommen. Im zweiten Jahr bekommt Anna 110€. Die 10€, die Anna im zweiten Jahr mehr Zinsen bekommt als im ersten Jahr, nennt man Zinseszins: Zinsen, die auf vorher bekommene Zinsen bezahlt werden. In anderen Worten: Die Leihgebühr für die höhere Summe Geld, die zum Teil aus früherer Leihgebühr besteht.
Am Anfang zeigt sich der Zinseszins kaum, insbesondere bei niedrigen Zinsen. Über die Zeit wirkt er aber immer stärker, wie du in dieser Grafik sehen kannst:
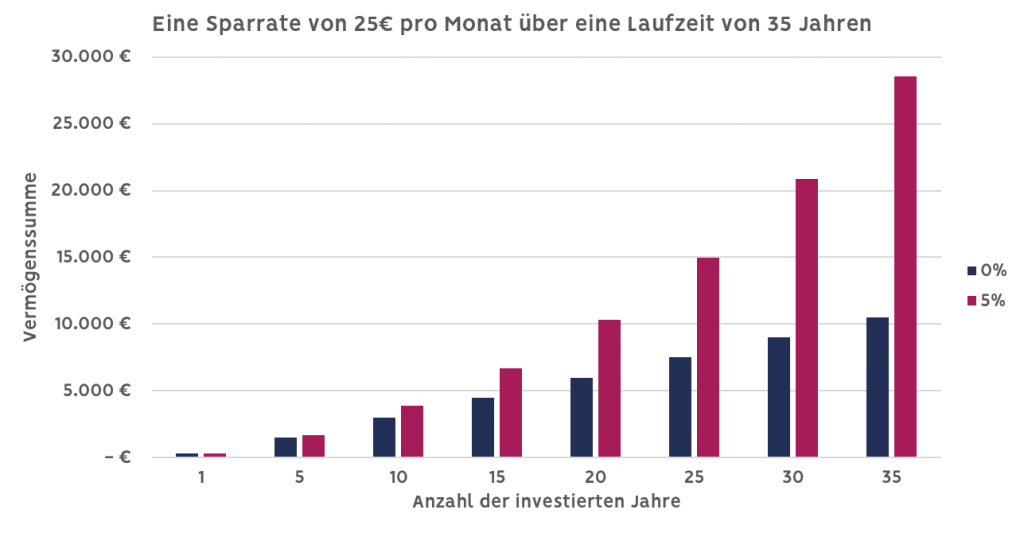
5% Unterschied in jährlichen Zinsen ergeben über eine lange Laufzeit eine riesige Differenz in der Summe, die du am Ende hast.
Die 72er-Regel
Die 72er-Regel ist eine hilfreiche Regel, um zu berechnen, wie stark der Zinseszins wirkt. Die Regel funktioniert wie folgt:
Teile 72 durch die Höhe der jährlichen Zinsen. Das Ergebnis ist die Anzahl der Jahre, die du warten musst, bis sich deine Investition verdoppelt hat.
Das Beispiel von oben sieht so aus:
72 / 10 = 7,2
Bei 10% Zinsen pro Jahr haben sich Annas 1.000€ nach etwas über 7 Jahren verdoppelt!
Momentan sind die Zinsen deutlich niedriger. So lange dauert es bei unterschiedlichen Zinssätzen, bis sich deine Investition verdoppelt hat:
0,01% Zinsen (aktuelle Zinsen bei vielen Tagesgeldkonten): 72 / 0,01 = 7200 Jahre
1% Zinsen: 72 / 1 = 72 Jahre
5% Zinsen: 72 / 5 = 14,4 Jahre
6% Zinsen: 72 / 6 = 12 Jahre
Diese einfache Regel zeigt, wie stark der Einfluss von Zinseszins ist und welchen Effekt schon 1% Unterschied in Zinsen hat.
Dein Geld zu sparen reicht nicht. In den nächsten Monaten geht es daher noch viel konkreter ums Investieren!
*Die Namen sind frei erfunden und haben keine Beziehung zu real existierenden Personen.

Guten Tag Claudia,
lieben Dank für die anschauliche Zinsberechnung. Der Wert 72 war mir kein Begriff aber jetzt. Hoffen wir, dass die Zinsen sich wieder mal positiv entwickeln.
Viele Grüße
Erika Walheim
Liebe Erika,
es freut mich, dass dir der Beitrag geholfen und gefallen hat! Ja, warten wir ab, wie sich das Zinsumfeld entwickelt…
Viele Grüße,
Claudia
Hallo Claudia! Danke für die Erklärung, ich glaube ich habe es jetzt verstanden. Und umso mehr verstehe ich jetzt, dass Sparbücher im Moment wirklich nichts taugen. 7200 Jahre will ich einfach nicht warten… Ute
Liebe Ute,
vielen Dank, das freut mich! Sparbücher sind wirklich zurzeit keine sinnvolle Investition – zumal die Inflation ja noch zusätzlich negativ wirkt.
Viele Grüße,
Claudia
Liebe Claudia und Team,
ich frage mich jetzt seit ich diesen Beitrag bei seiner ersten Erscheinung gelesen habe: Wäre es nicht schlau, wenn ich für meine Kinder und mich auf einem Depot zusammen spare? So haben wir insgesamt eine größere Einlegesumme, der Zins wäre höher und dadurch auch der Zinseszins. Natürlich stellt sich dann die Frage, wie man das am Ende wieder gerecht zurückverteilt sobald die Kinder eins nach dem anderen 18 werden, aber bevor ich mir darüber Gedanken mache, würde ich erst gerne wissen, ob meine Idee vollkommener Mumpitz ist, oder nicht.
Vielen lieben Dank!
Hi liebe Aline,
danke für deine Frage! Toll, dass du dich so nachhaltig mit deinen Finanzen beschäftigst 🙂
Vermutlich ist die Prozentrechnung hier etwas verwirrend. Tatsächlich ist es egal, ob du die Summe auf mehrere Depots verteilst oder alles in einem verwaltest, solange die Gesamtsumme identisch ist.
Als Beispiel:
Szenario 1: Du hast 100 € in einem Depot. Diese 100 € wachsen um 10 %. Ergebnis: Du hast 110 €.
Szenario 2: Du hast 100 €, aufgeteilt auf 2 Depots mit jeweils 50 €. Depot 1 wächst um 10 % –> 55 €. Depot 2 wächst ebenfalls um 10 % –> ebenfalls 55 €. In Summe: 110 €.
Solange also die Gesamtsumme identisch ist, ist es egal, auf wie viele Depots sie aufgeteilt ist.
Hat dir das geholfen?
Liebe Claudia,
Danke für deine Antwort! Beim Versuch meinen Hirnknoten anhand deines Beispiels zu verdeutlichen, fiel mir auf, dass tatsächlich der gesammelte Zinseszins der beiden 50€ Depots in Summe immer die gleichen Zinserträge erwirtschaften, als hätte ich nur das eine 100€ Depot. Ich hätte einfach mal mit einfachen Zahlen rechnen müssen 😅
Ich hab zwar immer noch das Gefühl, dass eine größere Einlegesumme mehr bringen müsste, als zwei kleine (bei gleichem Zinssatz), aber jetzt hab ich es schwarz auf weiß, dass mein Gefühl lieber den Mund hält. Zumindest in Mathe Sachen.
Danke nochmal!!
Ganz ehrlich: Sobald es um Zinsen geht, setzt bei mir das Gehirn auch aus 😀
Deshalb vertraue ich da immer den (Online-)Rechnern. Die Zahlen sprechen zum Glück eine klare Sprache.